清北學堂noip2018集訓D2
1 人贊了文章
## <center>清北學堂noip2018集訓D2</center>
>##### P.S.
>**今天講數據結構,大概包括了二叉堆,二叉搜索樹,線段樹,樹狀數組,並查集,st表,RMQ,LCA。**
## 二叉堆
- 基本功能
1. O(log n)插入元素
2. O(1)查最大(最小)元素
3. O(log n)刪除最大(最小)元素
4. O(log n)刪除任意元素
- 基本結構
- 最為常用的堆結構就是完全二叉堆。
- 在邏輯形式上,結構必須等同於完全二叉樹,同時,堆頂以外的每個節點都不大於(小於)其父親,即堆有序。
- 如果堆頂最大,稱為最大二叉堆(大根堆),反之稱為最小二叉堆(小根堆)。
- 因為完全二叉堆等同於完全二叉樹的結構,故高度相當。為O(log n).
- 一般為了實現方便,根節點編號為1,節點n左節點為2n,右節點為2n+1.
##### 查詢操作
- 最大(最小),直接返回堆頂即可。
##### 插入操作
- 首先把新元素插入向量末尾,為了維持堆的有序性,逐層檢查是否有序並調整,過程通常稱為上濾。
##### 建堆
- O(n log n)插入每個元素即可。
- O(n)?
- 先隨機放入一個完全二叉樹。
- 從倒數第二個深度開始檢索,使堆有序。
##### 刪除最大(最小)元素
- 將堆頂元素不斷下移,
##### 刪除任意元素
- 新建一個堆,將刪除的元素放入新堆里。即可實現刪除。
---
## 二叉搜索樹
- 基本功能
- 排序
- 查詢元素大小排名
- 插入元素
- 二叉平衡樹的基礎
- 結構
- 若左子樹不為空,則左子樹上所有節點小於根節點。
- 若右子樹不為空,則右子樹上所有節點大於根節點。
- 左右子樹也分別稱二叉排序樹。
- 排序
- 中序遍歷
- 查詢元素大小排次
- 從根開始向左、右是唯一的,如果向右,那麼將左邊的節點數加起來,反之不加。
- 插入
- 與查詢方法類似。
- 查詢到節點後向上更新其他節點。
---
## 線段樹
- 基本功能
- 建樹
- 單點查詢
- 單點修改
- 區間查詢
- 區間修改
- 結構
- 是一棵二叉搜索樹,每個節點代表一個區間。
- 每個節點需要維護
- 區間左右端點
- 區間要維護的信息
- 基本思想:二分
- 特殊性質
- 左子節點區間為[l,mid],右為[mid+1,r].
- 對於一個節點k,左子節點為2k,右子節點為2k+1.
- 建樹
- 對於二分的每一個節點,確定其代表的區間。
- 如果為葉子結點,存需要維護的信息。
- 對於非葉子結點,將兩個子節點狀態合併。
- 單點查詢
- 在左右節點搜索是確定的,由節點的mid決定,如果要查詢的點大於mid,則在右子樹搜索,反之在左子樹搜索。代碼如下:
```cpp
#include<bits/stdc++.h>
using namespace std;
#define LL long long
const int MAXN = 100000;
struct tree{
int l,r,s;
}mi[4*MAXN+20];
void build(int k,int l,int r){
mi[k].l=l;
mi[k].r=r;
if(l==r){
mi[k].s=r;
return;
}
int mid=(l+r)/2;
build(2*k,l,mid);
build(2*k+1,mid+1,r);
mi[k].s=mi[k*2].s+mi[k*2+1].s;
}
int search(int k,int n){
if(mi[k].l==mi[k].r&&mi[k].r==n){
return k;
}
int mid=(mi[k].l+mi[k].r)/2;
if(n<=mid) return search(k*2,n);
else return search(k*2+1,n);
}
int main(){
build(1,1,6);
cout<<search(1,5);
return 0;
}
```
- 單點修改
- 先執行單點搜索,然後執行修改操作,再向上更新狀態。
- 代碼如下
```cpp
int insert(int k,int n,int v){
int now=search(k,n);
mi[now].s+=v;
while(now!=1){
now/=2;
mi[now].s=mi[2*now].s+mi[2*now+1].s;
}
}
```
- 區間查詢
- 令[l,r]為當前節點代表的區間,mid代表區間中點,[x,y]代表要查詢的區間。
- 若[l,r]=[x,y]直接返回即可。
- 如果$yleq mid$,[l,r]->[l,mid],[x,y]不變,遞歸查詢。
- 如果$x > mid$,[l,r]->[mid+1,r],[x,y]不變,遞歸查詢。
- 否則,[x,y]跨過了mid的兩端,將其分成了兩個子問題,$[l,mid]$中查$[x,mid]$.$[mid+1,r]$中查$[mid+1,y]$.
- 代碼如下:
```cpp
int query_sum(int k,int x,int y){
if(y<mi[k].l||x>mi[k].r) return 0;
if(x==mi[k].l&&mi[k].r==y) return mi[k].s;
int mid=(mi[k].l+mi[k].r)/2;
return query_sum(k*2,x,mid)+query_sum(k*2+1,mid+1,y);
}
```
- 區間修改
- 關鍵:懶標記
- 經過節點的集合與區間查詢相同
- 更新這些區間的答案並打上一個標記,來表示這個區間中的數要進行哪些修改。
- 只有當查詢或者修改經過一個節點時,才將其節點上的懶標記放到兩個孩子節點,下放的同時修改兩個孩子節點的答案。
#### 模板(無區間修改)
```cpp
/*求和線段樹*/
#include<bits/stdc++.h>
using namespace std;
#define LL long long
#define inf 2147483647
const int MAXN = 100000;
struct tree{
int l,r,s;
}mi[4*MAXN+20];
void build(int k,int l,int r){
mi[k].l=l;
mi[k].r=r;
if(l==r){
mi[k].s=r;
return;
}
int mid=(l+r)/2;
build(2*k,l,mid);
build(2*k+1,mid+1,r);
mi[k].s=mi[k*2].s+mi[k*2+1].s;
}
int search(int k,int n){
if(mi[k].l==mi[k].r&&mi[k].r==n){
return k;
}
int mid=(mi[k].l+mi[k].r)/2;
if(n<=mid) return search(k*2,n);
else return search(k*2+1,n);
}
int query_sum(int k,int x,int y){
if(y<mi[k].l||x>mi[k].r) return 0;
if(x==mi[k].l&&mi[k].r==y) return mi[k].s;
int mid=(mi[k].l+mi[k].r)/2;
return query_sum(k*2,x,mid)+query_sum(k*2+1,mid+1,y);
}
int insert(int k,int n,int v){
int now=search(k,n);
mi[now].s+=v;
while(now!=1){
now/=2;
mi[now].s=mi[2*now].s+mi[2*now+1].s;
}
}
int main(){
int n,m,x,v;
cin>>n>>m>>x>>v;
build(1,n,m);
cout<<query_sum(1,x,v);
return 0;
}
```
---
## 樹狀數組
- 基本功能
- 單點修改,前綴信息查詢。
- 區間修改可減信息(前綴和),單點查詢。
- lowbit函數
- 含義:一個數,二進位表示中的最後一個1。
- 計算機中負數的表示?
- 怎麼求lowbit呢?
- $x and (-x)$
- 結構
- 我們定義c[i]為區間$[i-lowbit(i)+1,i]$。
- 怎麼直觀的看一看呢?
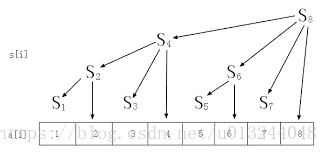
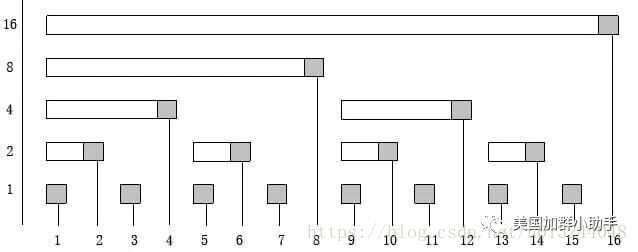
- $S_n=S_{(n-lowbit(n))}+C_n$
- 查詢代碼
```cpp
int sum(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=c[x];
return ans;
}
```
- 修改代碼
```cpp
void update(int x,int v){
for(;x<=n;x+=lowbit(x)) c[x]+=v;
}
```
- 代碼示例:
```cpp
#include<bits/stdc++.h>
using namespace std;
const int maxn=100010;
int a[maxn],c[maxn];
int n;
int lowbit(int x){
return x&(-x);
}
int sum(int x){
int ans=0;
for(;x;x-=lowbit(x)) ans+=c[x];
return ans;
}
void update(int x,int v){
for(;x<=n;x+=lowbit(x)) c[x]+=v;
}
int main(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
update(i,a[i]);
}
cout<<sum(n);
return 0;
}
```
- 區間修改,單點查詢
- 且以修改為加法,查詢為求和為例。
- 對於將$[l,r]$加$x$的操作,可以將點$l$加$x$,將點$r+1$減$x$,這時候求點$n$的前綴和就能得到點$n$真實的值。
---
## 並查集
- 基本功能
- 合併兩個集合
- 查詢某一個元素屬於哪個集合
- 結構
- 並查集S由若干子集合$S_i$構成,並查集的邏輯結構是一個森林。
- $S_i$表示森林中的一顆子樹。
- 一般以子樹的根作為該子樹的代表。
- 而對於並查集的存儲結構,可用一維數組來實現。
- 查詢某個元素屬於哪個集合
- 通常而言都是以根作為這個集合的代表元。
- 因此只需要不斷向父親節點走,直到走到根為止返回即可。
- 合併集合

- 路徑壓縮優化

- 示例代碼
```cpp
#include<bits/stdc++.h>
using namespace std;
int fa[200010];
int n;
int find(int x) {
if(fa[x] == 0) return x;
return fa[x] = find(fa[x]);
}
void add(int x,int y){
int xx=find(x),yy=find(y);
fa[yy]=xx;
}
int main(){
cin>>n;
int x,y,m,z;
for(int i=0;i<n;i++){
cin>>x>>y;
add(x,y);
}
cin>>m>>z;
cout<<find(m)<<" "<<find(z);
return 0;
}
```
---
## RMQ問題
- R——Range
- M——Minimum/Maximum
- Q——Query
- 即區間最值問題
### 例題

- 方法1:使用線段樹
- 方法2:st表
### ST表
- 基本功能
- $O(nlogn)$預處理,$O(1)$查詢區間最值。
- 結構
- $f[i][j]$表示區間$[i,i+2^j-1]$的信息。
- 整個$f$數組就是ST表。
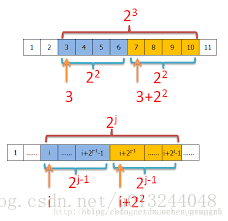
- 建表
- $f[i][0]$就是單點i的信息
- 當$j>0$時,$f[i][j]$為$f[i][j-1],f[i+2^{j-1}-1][j-1]$兩個區間信息的並集。
- 查詢
- 比方說我們要查詢區間$[x,y]$的信息。
- 令t為最大的正整數使得$2^tleq y-x+1$
- 那麼答案就是$[x,x+2^t-1]cup[y-2^t+1,y]$
- 代碼如下:
```cpp
#include<bits/stdc++.h>
#define maxn 111100
#define logN 25
//因為cmath中的log函數效率差,不如直接設定一個永遠到不了的值
using namespace std;
int f[maxn][logN],a[maxn],n,m;
void pre_st(){ //製表
for(int i=1;i<=n;i++)
f[i][0]=a[i]; //因為第二個框框中存的j是用來計算 i+2^j-1(既該f保存的值)
//服務於動態規劃的結果
for(int j=1;j<=logN;j++){
for(int i=1;i+(1<<j)-1<=n;i++)
f[i][j]=max(f[i][j-1],f[i+(1<<j-1)][j-1]); //注釋1 (1<<j)是計算出 2^j 把一一直右移即可得到
//注釋2 使用剛才得到的動態規劃方程
}
}
int main(){
cin >> n;cin >> m;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
pre_st(); //製表
int x,y;
for(int i=1;i<=m;i++){
cin >> x >> y;
int s=log(y-x+1)/log(2); //計算出這一段距離之中最大的2的倍數,以查表
cout << max(f[x][s],f[y-(1<<s)+1][s]) << endl;; //合併左右不分的解
}
return 0;
}
```
---
## 查詢樹上兩點的最近公共祖先(LCA)
- L——Lowest
- C——Common
- A——Ancestor
- 即最近公共祖先
### 歐拉序
- 一種特殊的dfs序,每到達一個點就加入序列。
- 記錄每個點第一次出現的時間$S[u]$,歐拉序中第i個點為$Q[i]$。
- $LCA(x,y)$是$Q[S[x]...S[y]]$中層數最低的點。
- 區間最值?
- ST表!
推薦閱讀:
TAG:數學 |
