機器學習演算法實踐-樸素貝葉斯(Naive Bayes)

前言

上一篇總結了決策樹的實現，本文中我將一步步實現一個樸素貝葉斯分類器，並採用SMS垃圾簡訊語料庫中的數據進行模型訓練，對垃圾簡訊進行過濾，在最後對分類的錯誤率進行了計算。

正文

與決策樹分類和k近鄰分類演算法不同，貝葉斯分類主要藉助概率論的知識來通過比較提供的數據屬於每個類型的條件概率, 將他們分別計算出來然後預測具有最大條件概率的那個類別是最後的類別。當然樣本越多我們統計的不同類型的特徵值分布就越準確，使用此分布進行預測則會更加準確。

貝葉斯準則

樸素貝葉斯分類器中最核心的便是貝葉斯準則，他用如下的公式表示:

此公式表示兩個互換的條件概率之間的關係，他們通過聯合概率關聯起來，這樣使得我們知道p(B|A)p(B|A)的情況下去計算p(A|B)p(A|B)成為了可能，而我們的貝葉斯模型便是通過貝葉斯準則去計算某個樣本在不同類別條件下的條件概率並取具有最大條件概率的那個類型作為分類的預測結果。

使用條件概率來進行分類

這裡我通俗的介紹下如何通過條件概率來進行分類，假設我們看到了一個人的背影，想通過他背影的一些特徵(數據)來判斷這個人的性別(類別)，假設其中涉及到的特徵有: 是否是長發, 身高是否在170以上，腿細，是否穿裙子。當我們看到一個背影便會得到一個特徵向量用來描述上述特徵(1表示是，0表示否): ω=[0,1,1,0]

貝葉斯分類便是比較如下兩個條件概率:

1. p(男生|ω)，ωω 等於 [0,1,1,0] 的條件下此人是男生的概率
2. p(女生|ω)，ωω 等於 [0,1,1,0] 的條件下此人是女生的概率

若p(男生|ω)>p(女生|ω), 則判定此人為男生, 否則為女生

那麼p(男生|ω) 怎麼求呢? 這就要上貝葉斯準則了

根據貝葉斯準則 (知乎的公式不能顯示中文的嗎 -_-!)，

寫成好理解些的便是:

如果特徵之間都是相互獨立的(條件獨立性假設)，那麼便可以將上述條件概率改寫成:

這樣我們就能計算當前這個背影屬於男生和屬於女生的條件概率了。

實現自己的貝葉斯分類器

貝葉斯分類器實現起來非常的簡單, 下面我以進行文本分類為目的使用Python實現一個樸素貝葉斯文本分類器.

為了計算條件概率，我們需要計算各個特徵的在不同類別下的條件概率以及類型的邊際概率，這就需要我們通過大量的訓練數據進行統計獲取近似值了，這也就是我們訓練我們樸素貝葉斯模型的過程.

針對不同的文本，我們可以將所有出現的單詞作為數據特徵向量，統計每個文本中出現詞條的數目(或者是否出現某個詞條)作為數據向量。這樣一個文本就可以處理成一個整數列表，並且長度是所有詞條的數目，這個向量也許會很長，用於本文的數據集中的簡訊詞條大概一共3000多個單詞。

def get_doc_vector(words, vocabulary): """ 根據辭彙表將文檔中的詞條轉換成文檔向量 :param words: 文檔中的詞條列表 :type words: list of str :param vocabulary: 總的辭彙列表 :type vocabulary: list of str :return doc_vect: 用於貝葉斯分析的文檔向量 :type doc_vect: list of int """ doc_vect = [0]*len(vocabulary) for word in words: if word in vocabulary: idx = vocabulary.index(word) doc_vect[idx] = 1 return doc_vect

統計訓練的過程的代碼實現如下:

def train(self, dataset, classes): """ 訓練樸素貝葉斯模型 :param dataset: 所有的文檔數據向量 :type dataset: MxN matrix containing all doc vectors. :param classes: 所有文檔的類型 :type classes: 1xN list :return cond_probs: 訓練得到的條件概率矩陣 :type cond_probs: dict :return cls_probs: 各種類型的概率 :type cls_probs: dict """ # 按照不同類型記性分類 sub_datasets = defaultdict(lambda: []) cls_cnt = defaultdict(lambda: 0) for doc_vect, cls in zip(dataset, classes): sub_datasets[cls].append(doc_vect) cls_cnt[cls] += 1 # 計算類型概率 cls_probs = {k: v/len(classes) for k, v in cls_cnt.items()} # 計算不同類型的條件概率 cond_probs = {} dataset = np.array(dataset) for cls, sub_dataset in sub_datasets.items(): sub_dataset = np.array(sub_dataset) # Improve the classifier. cond_prob_vect = np.log((np.sum(sub_dataset, axis=0) + 1)/(np.sum(dataset) + 2)) cond_probs[cls] = cond_prob_vect return cond_probs, cls_probs

注意這裡對於基本的條件概率直接相乘有兩處改進:

1. 各個特徵的概率初始值為1，分母上統計的某一類型的樣本總數的初始值是1，這是為了避免如果有一個特徵統計的概率為0，則聯合概率也為零那自然沒有什麼意義了, 如果訓練樣本足夠大時，並不會對比較結果產生影響.
2. 由於各個獨立特徵的概率都是小於1的數，累積起來必然會是個更小的書，這會遇到浮點數下溢的問題，因此在這裡我們對所有的概率都取了對數處理，這樣在保證不會有損失的情況下避免了下溢的問題。

獲取了統計概率信息後，我們便可以通過貝葉斯準則預測我們數據的類型了，這裡我並沒有直接計算每種情況的概率，而是通過統計得到的向量與數據向量進行內積獲取條件概率的相對值並進行相對比較做出決策的。

def classify(self, doc_vect, cond_probs, cls_probs): """ 使用樸素貝葉斯將doc_vect進行分類. """ pred_probs = {} for cls, cls_prob in cls_probs.items(): cond_prob_vect = cond_probs[cls] pred_probs[cls] = np.sum(cond_prob_vect*doc_vect) + np.log(cls_prob) return max(pred_probs, key=pred_probs.get)

進行簡訊分類

已經構建好了樸素貝葉斯模型，我們就可以使用此模型來統計數據並用來預測了。這裡我使用了SMS垃圾簡訊語料庫中的垃圾簡訊數據, 並隨機抽取90%的數據作為訓練數據，剩下10%的數據作為測試數據來測試我們的貝葉斯模型預測的準確性。

當然在建立模型前我們需要將數據處理成模型能夠處理的格式:

ENCODING = "ISO-8859-1"TRAIN_PERCENTAGE = 0.9def get_doc_vector(words, vocabulary): """ 根據辭彙表將文檔中的詞條轉換成文檔向量 :param words: 文檔中的詞條列表 :type words: list of str :param vocabulary: 總的辭彙列表 :type vocabulary: list of str :return doc_vect: 用於貝葉斯分析的文檔向量 :type doc_vect: list of int """ doc_vect = [0]*len(vocabulary) for word in words: if word in vocabulary: idx = vocabulary.index(word) doc_vect[idx] = 1 return doc_vectdef parse_line(line): """ 解析數據集中的每一行返回詞條向量和簡訊類型. """ cls = line.split(",")[-1].strip() content = ",".join(line.split(",")[: -1]) word_vect = [word.lower() for word in re.split(r"W+", content) if word] return word_vect, clsdef parse_file(filename): """ 解析文件中的數據 """ vocabulary, word_vects, classes = [], [], [] with open(filename, "r", encoding=ENCODING) as f: for line in f: if line: word_vect, cls = parse_line(line) vocabulary.extend(word_vect) word_vects.append(word_vect) classes.append(cls) vocabulary = list(set(vocabulary)) return vocabulary, word_vects, classes

有了上面三個函數我們就可以直接將我們的文本轉換成模型需要的數據向量，之後我們就可以劃分數據集並將訓練數據集給貝葉斯模型進行統計。

# 訓練數據 & 測試數據ntest = int(len(classes)*(1-TRAIN_PERCENTAGE))test_word_vects = []test_classes = []for i in range(ntest): idx = random.randint(0, len(word_vects)-1) test_word_vects.append(word_vects.pop(idx)) test_classes.append(classes.pop(idx))train_word_vects = word_vectstrain_classes = classestrain_dataset = [get_doc_vector(words, vocabulary) for words in train_word_vects]

訓練模型:

cond_probs, cls_probs = clf.train(train_dataset, train_classes)

剩下我們用測試數據來測試我們貝葉斯模型的預測準確度:

# 測試模型error = 0for test_word_vect, test_cls in zip(test_word_vects, test_classes): test_data = get_doc_vector(test_word_vect, vocabulary) pred_cls = clf.classify(test_data, cond_probs, cls_probs) if test_cls != pred_cls: print("Predict: {} -- Actual: {}".format(pred_cls, test_cls)) error += 1print("Error Rate: {}".format(error/len(test_classes)))

隨機測了四組，錯誤率分別為:0, 0.037, 0.015, 0. 平均錯誤率為1.3%

測完了我們嘗試下看看不同類型簡訊各個詞條的概率分布是怎樣的吧:

# 繪製不同類型的概率分布曲線fig = plt.figure()ax = fig.add_subplot(111)for cls, probs in cond_probs.items(): ax.scatter(np.arange(0, len(probs)), probs*cls_probs[cls], label=cls, alpha=0.3) ax.legend()plt.show()

試試決策樹

上一篇我們基於ID3演算法實現了決策樹，同樣是分類問題，我們同樣可以使用我們的文本數據來構建用於分類簡訊的決策樹，當然唯一比較麻煩的地方在於如果按照與貝葉斯相同的向量作為數據，則屬性可能會非常多，我們在構建決策樹的時候每層樹結構都是遞歸通過遍歷屬性根據信息增益來選取最佳屬性進行樹分裂的，這樣很多的屬性可能會對構建決策樹這一過程來說會比較耗時.那我們就試試吧…

# 生成決策樹if not os.path.exists("sms_tree.pkl"): clf.create_tree(train_dataset, train_classes, vocabulary) clf.dump_tree("sms_tree.pkl")else: clf.load_tree("sms_tree.pkl")# 測試模型error = 0for test_word_vect, test_cls in zip(test_word_vects, test_classes): test_data = get_doc_vector(test_word_vect, vocabulary) pred_cls = clf.classify(test_data, feat_names=vocabulary) if test_cls != pred_cls: print("Predict: {} -- Actual: {}".format(pred_cls, test_cls)) error += 1print("Error Rate: {}".format(error/len(test_classes)))

隨機測了兩次，錯誤率分別為:0.09, 0.0

效果還算不錯

我們還是用Graphviz可視化看一下決策樹都選取了那些詞條作為判別標準(這時候決策樹的好處就體現出來了)。

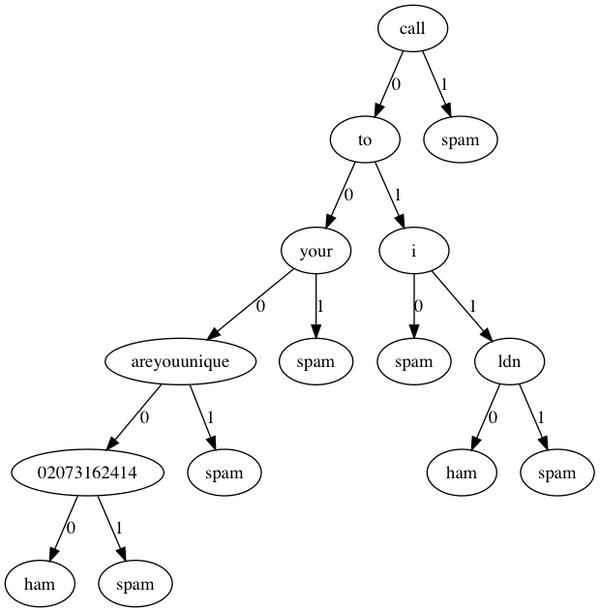
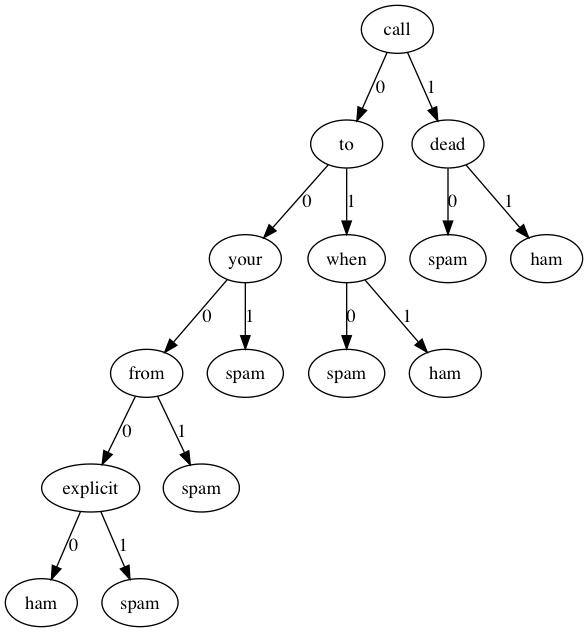
可見決策樹的深度並不是很深，如果分類類型一多，估計深度增加上去決策樹可能會有些麻煩。

總結

本文我們使用Python一步步實現了樸素貝葉斯分類器，並對簡訊進行了垃圾簡訊過濾，同樣的數據我們同決策樹的分類效果進行了簡單的比較。本文相關代碼實現:https://github.com/PytLab/MLBox/tree/master/naive_bayes 。決策樹過濾垃圾簡訊的腳本在https://github.com/PytLab/MLBox/tree/master/decision_tree

參考

• 《Machine Learning in Action》
• 實例詳解貝葉斯推理的原理
• 大道至簡：樸素貝葉斯分類器

推薦閱讀：