兩個速度為一米每秒的物體相撞和一個速度為2米每秒的物體撞一個靜止物體 破壞程度相同嗎?
假設以上所有物體質量相等。一切為理想條件
很高興碰到中學物理題,技癢來答,順便看看評論區感慨一下物理科普任重道遠,義務教育遠未成功。
如果是真空中對撞,和其他參照物不發生關係,破壞絕對相同。實際上,如果沒有第三方參照物,你根本就無法判斷到底是兩個物體相向飛行,還是一個物體靜止,另一個撞上來。
當然,我知道你的疑惑在哪裡。
從邏輯說,動能公式是:E=1/2mv^2 ,和質量的一次方成正比,和速度的二次方成正比。假設兩個物體的質量都是1。兩個速度為1米每秒的物體,動能之和為1;一個2米每秒的物體,動能是2。動能是破壞的根源,動能不一樣,為啥破壞會一樣呢?因為你忽略了碰撞後的殘餘動能。
我們假設是完全非彈性碰撞,損失的動能完全用來破壞物體。
在第一個「對撞」的參照系下,碰撞後動能為0,動量也為0。兩個物體完全靜止,用來破壞的動能恰好是1。在第二個「單向撞」的參照系下,碰撞之後,有共同速度1,動量為2,兩個物體合併在一起,質量為2,以速度1飛行。動能是1/2mv^2 現在m是2,v是1,E等於1。看到了嗎,在這個參照系下,碰撞後依然保留了動能1,你損失的動能是2-1=1,和前面那個參照系的相等。既然損失動能相等,碰撞造成的破壞也相等。從感性認識說,一個時速120公里的車撞靜止的車,造成的破壞的確比兩個60公里的車對撞要大。為什麼呢?因為時速都是相對地球的,而車禍之後,所有的車最後都要停下來,變成和地球相對為0的速度,所有的動能都要轉化為破壞。這種情況下,時速120的一輛車,動能大於時速60的兩輛車,最後造成的破壞肯定也更大。如果憑著這種感性認識,認為速度為2的碰撞損失更大,是會做錯題的。因為你在感性分析中忽略了現實中車禍要多出來的步驟——碰撞後所有碎片的速度都要相對地面歸零。而在你的題目中,碰撞後的速度是不必歸零的。

雖然我不是結構或者物理的專業人士,但是,在慣性系中物理定律不是不變嗎,變換個坐標系不就是一樣了。
Google對Galilean invariance解釋是這樣的。- Galilean invariance or Galileanrelativity states that the laws of motion are the same in all inertial frames.
所以雖然模擬結果有,但我仍然不能理解@豬小寶的回答。我覺得是計算錯誤。是不是他的計算模型不符合galilean invariance?
理想狀態下是一樣的。用牛頓或者相對論都可以得到(這裡忽略速度合成公式帶來的微小差異。)
但是生活中並沒有理想情況。相對於空氣的速度,加速過程中引起的影響,實驗設備引起的不對等的摩擦以及「相同」物體的微小差異,這些都是不可避免的。
當然視角放寬一點的話,這樣的理想情況也是找得到的。在粒子對撞上,題主所說的兩種情況是完全一樣的。實名反對 @豬小寶 的高票回答: 兩種情況下子彈的受損情況不一樣。
(豬小寶已經把他的原回答刪除了。)如果這個結論是對的, 那麼我們將得到一個違反物理學基本原理的推論: 我在不同的慣性系參照系裡面觀察,子彈的受損情況不同。觀察者的主觀選取慣性參照系的行為將影響客觀的子彈受損情況,這顯然是荒謬的。當然在量子力學的情況下會出現主觀的觀測行為影響波函數的現象,但是這不是我們這裡討論的問題。我認為答案應該是,兩種情況下子彈的受損情況完全一樣。
中學物理是幼稚,但是不代表中學物理就不是真理。工科裡面的確要考慮到很多實際的問題,但是工科的結論不應該違反基本的物理學原理。高票答主並沒有做過實驗,而只是做了數值模擬,然後在沒有仔細推敲的情況下認為數值模擬的結果就一定是真實情況,這實在是缺乏科研應該有的嚴謹態度。我也是做工科的,我也做很多數值模擬,但是很多時候數值模擬的結果並不正確。當一個數值模擬的結果明顯不符合基本物理學原理的時候,應該去找出數值模擬的錯誤在哪裡,而不是動搖基本的物理學原理。不回答題主的問題,我認為大家這麼積極的討論過後,題主也應該得出了自己的結論
某位高大上的回答用了很多很厲害的圖片和分析來說明這兩種情況是不一樣的,從科普的角度來說,給廣大圍觀群眾展示了有限元分析的威力,也普及了材料力學的常識,但是我認為他的回答存在幾點問題:
首先,相對論到底在這個問題中適不適用?在真空中,我在靜止(0m/s)的情況下看到兩個500m/s的子彈對撞,和我以500m/s的速度移動的情況下看1000m/s的子彈撞靜止(0m/s)的子彈,如果結局是兩種碰撞破壞不一樣,我只能說我幼小的心靈受到了1億點傷害
對於以上這種局面,畢竟世界上不是只有中學物理和相對論的,在這兩者之間還有實用的工程科學嘛
那實用的工程科學應該怎麼分析呢?用有限元工程模擬呀
問題就來了,這模擬出來的結果是不一樣可怎麼辦?
兩種可能:1.肯定是在實際的情況中出現了某種我們在理想假設下沒考慮到的影響因素,這種因素有可能是我們平時不了解的或者沒有想到的
2.模擬軟體算錯了這位同志顯然認為是第一種可能,所以談到了材料的力學性能與載入速度之間的關係,認為:儘管耗散的能量的大小類似,但是因為撞擊速度的不同,導致這些能量耗散在了不同的部位,從而體現為不同的變形和破壞形式。
然而在這裡,撞擊速度的不同這幾個字就很詭異,因為兩種情況的相對速度是一毛一樣的,所以我並沒有理解到他的意思,請大家開導我
對於這種理想模型的思考,我認為本來就不應該使用工程軟體來模擬,要理想就用理論,要實際就用實驗
而使用工程軟體,誰也無法保證不發生計算錯誤
當發生計算錯誤之後,如果不是承認軟體的缺陷,有些概念確實和問題有關,但是這些概念絕對不是這兩種情況的關鍵區別,生拉硬扯這些概念來自圓其說,難免誤導圍觀群眾高中物競坑:對於兩個系統來說。總能量不同,但是相對質心的資用能相同(資用能這個概念念可自行百度,這是重點)。。這樣(質量相同)碰撞完全消耗資用能,效果是一樣的。在一個2V的粒子撞靜止靶子的情況中,多出的一部分能量成為了質心能量不因碰撞被消耗。(叫它沒用能~)————————————————————關於這個的應用,比如對撞機!。把一個粒子加速到一個高速2V撞擊一個靜止粒子靶子比 把兩個粒子加速到V消耗的能量大許多,所需的加速器的體積也大許多。所以一般採用兩個粒子加速起來對撞相關的百度上也是挺清晰吧.
我想為 @馬前卒 的回答提供一下簡單的推導。
假定兩個物體質量分別為m1和m2,直線運動,初速度分別是v1(向量)和v2(向量),末速度v3(向量)。
推導過程見圖片。

先說結論:碰撞時及碰撞後瞬間效果一樣。 但碰撞完成後, 各自和地面關係不一樣。
我是學微觀物理的。 在研究粒子碰撞和相互作用時(比如:核反應), 最為方便的是採用「質心系 center of mass frame」 參考坐標系。 這是樣對於「實驗室系(laboratory frame)」參考坐標系來說的。 L系是假設實驗室靜止, 粒子取相對於實驗室的速度, C系則是使得考察系統的動量為0, 這樣碰撞後系統的總動量自然也是0, 無論是彈性碰撞, 還是非彈性碰撞, 甚至核反應, 都一樣, 總動量為0. 而且, 質心系體現一個事實, 即物理規律與選取非參考點無關, 只在乎封閉系統自身。 (此處暫時省略1000字)
把質心系應用到「兩個速度為v」的相同物體相撞, 與一個2v 一個靜止相撞這個案例, 是這樣的:
第一種情形下, 質心相對於實驗室速度為0, 碰撞之後, 兩者相對於實驗室及質心的速度均為0, 因此兩球瞬間動量損失的絕對值均為 為 mv. 相對於地面實驗室, 均靜止了。
第二種情形, 質心相對實驗室速度為 v, 碰撞後, 兩球在質心繫動量為0, 相對地面為均 v, 因此兩球瞬間損失動量絕對值均為 mv. 即:兩車交換了速度。
就碰撞來說, 動量轉移才是破壞因素。 因此,兩種情形既然都轉移了mv 的動量, 那麼碰撞的後果是一樣的。
差別還是有的, 第一種情形, 兩車都靜止了, 但第二種情形, 原先靜止的車, 碰撞後速度為2v,即還沒停下來, 當然有附加風險。 但這風險,應該不是題主考察範圍。
再舉個單車碰地球, 地球質量無窮大, 車么, 算2噸吧。 所以這時質心繫和實驗室系幾乎重合到地心。單車以v 撞上牆(與地球牢牢固定), 以-v 彈回, 瞬間獲得2mv動量。
兩者以v 對碰, 都靜止了, 瞬間轉移 mv 的動量.
是不是所有和課本上不符合的結論,都會更受歡迎?特別是貌似翔實的答案?
算是人性了,看到和自己長期相信的東西不一致,下意識的會驚訝,然後看著對面複雜的參數+圖圖圖就直接繳械投降了。本來沒啥好回答的,不過被人拉黑+屏蔽+刪評論這是頭一遭,先佔坑,研究一下再來回答。看看是不是那位高大上的各種圖的同學漏掉了什麼。之前拉黑我的估計會有幾個x權主義者我不在意,不過這種科學問題應該有明確結果的,不應該會有這麼大的分歧。
我想知道的是,那應力和初速度的關係中,初速度的參考系是啥?
材料的應力和載入速度有關,那得出載入速度需要一個參考系。如果我選一個正在天空中flying的飛機作為參考系,是不是載入速度就變得老高了?這簡單的換個參考系,材料的應力就變了?要是這樣您看,假設我有個被子,在載入速度=100m/s的時候一碰就碎,那天上飛過一架飛機(或者導彈或者火箭什麼的)正好這個速度,那以那玩意兒為參考系,我這杯子是不是一碰就碎?
看似高大上的模型+圖片,我覺得並沒有解釋這個問題。視頻放上來:
 impact視頻
impact視頻 impact視頻
impact視頻
其實這個問題深究起來可以一直深究下去,就損傷而言比如整車的碰撞傷害的就不光是車的強度問題了,因為乘員對加速度也是有承受極限的,所以我在這裡對問題做進一步具體然後用有限元的數值方法模擬。
如果要考察撞擊後的傷害值,肯定是要考慮撞體的材料性質的,那就假設為最簡單的彈性體,在我這裡模型被具體量化,所有柱體的質量7E-6噸,一倍速率V=8m/s, 兩倍速率 2V=16m/s,
完全是理想化的碰撞,只考慮接觸中可能的滑動摩擦。
柱體材料也是簡化的彈性模型,彈性階段性質與橡膠材料基本相似。
為什麼這樣做,因為說到傷害本質上還是結構受力導致的,只是碰撞的受力的時間相對較短而且如果是硬材料在這速度下變形也會很小,那麼對於整個能量轉化的過程看的就不明顯,所以選用軟材料,方便觀察變形發生的過程。
就題主的問題而言,碰撞物的傷害,這裡從兩個指標進行衡量:
1,)整個碰撞過程中軟體內發生的最大應力(關於應力可以打個不恰當的比喻,
如果把碰撞比喻成兩軍交戰,那麼應力最大的地方就相當于軍隊中最先負傷的分隊,
至於有沒有被K.O掉那就要看他們的扛打能力了,反映回去就是材料的一個損傷極限),這樣從一個局部就可以反映出碰撞體的傷害情況。
2.)另一個是從撞體全局來看,在碰撞過程中柱體所發生的最大形變,
具體指標是以軟柱體在撞擊方向首尾兩端所發生的相對位移的最大值,有沒有潰不成軍。
好的,下面我稍微詳盡下簡化模型:
第一組是等速率(8m/s)相向而撞得等質量軟柱體,分別編號1與2
第二組是等質量編號3軟柱體以上一組的兩倍速率(16m/s)撞向等質量靜止的軟柱體4.
FE(有限元)簡化模型如下:


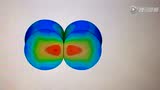
再看碰撞最深處時兩組柱體的應力分布,感官上就能發現應力雲圖分布基本一致。最大應力值分別是2MPa與2.1MPa。結果看到這裡兩組表現都是一致的。
下面再看柱體的形變情況:

這裡可以看到即便取用了橡膠材料的彈性段來模擬,整個碰撞的過程時間還是很短,基本在0.001ms以內碰撞中能量的轉換就已經完成了。四個柱體的最大變形參考指標基本一致。這裡插一句,其實對於數值模擬而言,小數點後面的數字不具有太大的參考意義。
那麼看到這裡,兩組結果還是完全一致的。那麼有沒有不一致的地方呢,往下看:

那麼從有限元模擬的結果來看,無論是單個軟體內部的應力狀態,還是撞擊中軟體的最大形變狀態四個軟體的結果基本上在計入數值誤差範圍內是完全一致的,所以損傷而言可以說是完全一致的,唯一不同的地方是撞擊過後每個個體之間的運動狀態存在各自不同,整個過程從單個柱體的角度去看能量的轉化方式有不同,但條條大路通羅馬。
其實還有動畫,看起來更直觀,不知道知乎怎麼傳動畫。
我覺得有一種簡單的理解:以其中一個物體為參照系,無論該物體以多大的絕對速度運動,其相對速度始終為0。另一物體相對此參照系的相對速度也是一個定值,無論其絕對速度有多大。因此在此參照系下,碰撞產生的效果是始終相同的(不討論碰撞的結果,因為剛體和彈性體等多種體在碰撞下的結果不盡相同。)而且此參照系具有普遍性,可以是任何一個物體,在普遍的參照系下,所討論的兩個物體均具有相同的相對速度,因此碰撞產生的效果,和參照系無關,只和相對速度有關。
在如果速度是在慣性系下測量的,那麼試驗結果一定相同,和兩個物體材料甚至質量都沒有關係。
這個問題只需要伽利略原理都能夠解釋清楚。物理定律在一切慣性參考系中具有相同的形式,任何力學實驗都不能區分靜止和勻速運動的慣性參考系。(相對性原理)
注意,任何力學試驗。
@馬前卒 已經說的很好了如果是真空中對撞,和其他參照物不發生關係,破壞絕對相同。實際上,如果沒有第三方參照物,你根本就無法判斷到底是兩個物體相向飛行,還是一個物體靜止,另一個撞上來。
這兩個力學試驗實質上只有參考系取的不同而已,如果他們的試驗結果不同的話,那就是推翻了伽利略原理。
推翻伽利略原理並不是不可能,不過推翻它,恐怕沒這麼簡單。============看到豬小寶又更新了一段:這兩者的對比跟伽利略的相對性原理沒有關係,並且不矛盾。
一個物理實驗,實驗的內容為控制適當的裝藥量,從而做到發射500米每秒的子彈對撞,對比加大裝藥量之後,發射1000米每秒的子彈撞擊靜止的子彈,實驗結果是這兩種情況的結果可能並不相同。這個實驗在哪裡做,結果都是「這兩個情況的碰撞結果有區別」這個結果,不管在地面上、火車裡、飛機里、或者伽利略想的勻速運動的輪船船艙里。這才是伽利略的相對性。
看過豬小寶同學很多回答,回答通常有理有據。然而都博士了不可能不知道相對性是什麼,為了避免豬同學揣著明白裝糊塗把看客真的搞糊塗了,還是解釋下。
1.
怎麼可能沒有關係!承認相對性原理,那麼根本就沒有兩種情況,在子彈出膛之後這壓根就是一種情況。出膛之後,相對於兩顆子彈的公共質心這個參考系,所謂的「兩種情況」是完全一致的。要不然請告訴我他們哪些物理參數不同?(注意在沒有外力的情況下,「兩顆子彈的公共質心」這個參考系確實是一個慣性系,這裡選用這個參考系是為了方便)2.不管在地面上、火車裡、飛機里、或者伽利略想的勻速運動的輪船船艙里
這句話其實有一定誤導性,指導人們選擇地面、火車、飛機、輪船為參照系,而不是例如「相撞前【其中一顆子彈的質心及其慣性延續】」,或者「【相對於地面速度】與【子彈初速度】相等的【參考系】」。
3.
豬同學舉例的內容控制的變數是裝葯化學能,爆炸後理想條件完全轉化成動能,從而控制速度。然而豬同學這裡利用了同學們通常忘記的事情,即動能也是相對的,相對不同參考系也會有不同,還請大家注意。4.
按照豬小寶同學的思路繼續,如果在槍AB相對靜止的情況下A子彈出膛速率1000m/s向右,B子彈出膛速率0(均相對於慣性系X),這時我們只需要選擇一個相對於慣性系X以500m/s向右移動的慣性系Y,就可以達成AB子彈相對於Y各自以500m/s速度相向運動。顯然實驗結果並無不同。5.這麼基本的東西我廢話這麼多我一定是閑的蛋疼然而這麼基本的東西竟然在知乎上還有這麼多人搞不清楚真是有點震驚這一道題………真是暴露了好多人的物理水平……
然後來答題 題主的理想情況沒有給清楚,中學題的理想情況是糊弄人的,但中學的物理可不是糊弄人的。和樓下很多答主一樣,在真空中,如果物體不因為加速過程產生任何變化,那麼你根本無法區別這兩種情況。 伽里略相對性,是說換系的時候速度直接加,所以伽里略變換下這兩個物理情況是完全相同的,伽里略變換是牛頓力學的基礎,和任何模型沒有任何關係 然後為什麼說經典力學不準確就要扯相對論?扯相對論?扯相對論?1000m每秒的速度扯相對論?那就點一下,狹相是採用洛倫茲變換,是說換系的時候速度不能直接加,也就是說地面上這倆情況不等價了,等價的情況在地面上看會比較反直覺,僅此而已 同學們,普物該重學了我覺得可以用一下幾句話來總結:
1、經典問題下,牛頓力學的那一套,包括能量守恆,動量守恆,伽利略變換不影響物理過程,是不可懷疑的!
2、各種經典的應用力學,是牛頓力學與物性的結合,能被挑戰的理論其實叫模型,牛頓那一套不可挑戰。3、經典的問題,如果計算或者實驗與牛頓力學衝突,那肯定是計算或者實驗有問題。其實回答的主要原因是想到一個很好的思考題,是李俊鋒老師在理論力學課上提出來的,我剛開始竟然想錯了2333……很狡猾~
說現在有一個雞蛋固定住,一個雞蛋碰撞它。我們知道力與反作用力大小相等,那看起來兩個雞蛋破碎的難易程度是一樣的……真的是這樣嗎?我在評論區有簡單的解釋,大家有別的想法可以和我討論這個問題……我應該強調一下,本回答強調的是物理定律本身內涵的對稱性,即參考系變換下不變。
但是事實上由於實際情景下的複雜性,動撞靜和對撞一般不能看做可以通過參考系變換互相轉化的,所以在實際狀況下(比如子彈,撞車)一般破壞不同。
————————分割線————————
在這樣簡單理想的問題情景下,問題完全可以用基本的物理學原理來解釋。
根據情景設定,兩個情景下物體都不受外在環境作用,兩個情景可以通過坐標系變換互相轉化。
再根據狹義相對性原理,在(慣性的)參考系變換下,物理定律保持不變。
兩個情景,相當於從兩個參考系裡去看同樣的一件事。
所以撞完都一樣,包括所謂"破壞效果"。
你可以用牛頓定律驗算一遍,兩個物體對撞完再坐標變換的結果,和2倍速度撞擊靜止物體直接得到的結果。
結果都是相同的。因為牛頓定律是遵循狹義相對性原理的。假設以上三個物體質量相等
還是信息不足,因為:
- 如果三個物體質量相等,但結構材質不相等,也會造成不同的結果。
- 就算三個物體在各方面都完全相等,第四個靜止的物體是怎麼回事你不說,那也無法得出單一結果。
- 就算四個物體在各方面都完全相等,第四個靜止的物體是沒有固定僅僅靜止,還是固定在地上,依然會造成不同的結果。
- 假設四個物體在各方面都完全相等,並且第四個物體沒有固定,那麼根據原問題提出的條件,破壞程度是大致相同的。如果第四個物體有固定,則2m/s撞固定物的破壞程度要明顯高於1m/s的對撞。
速度不都是相對的嗎…
在一個相對於地面速度為1米每秒的小車上,有兩個小球以相對於地面1米每秒的速度對撞,車外的人(以地面為參考系)看到的就是一種情況,車上的人(以車為參考系)看到的就是第二種情況。碰撞完全一樣,只是參考系不同。
現實情況下,個人認為兩物體從相撞到相對靜止這個過程是完全相同的,但是第二種情況兩物體會繼續運動,直到靜止,可以看做是二段傷害吧。系統可分為質心動能和相對動能(具體請查閱克尼希定理),由於動量守恆,碰撞所能轉化的能量只有相對動能,質心動能不能轉化。前者的質心動能為0,相對動能為2個單位,後者的質心動能為2個單位,相對動能也是2個單位。雖然總動能不同,而碰撞轉化能量是相同的,所以兩者的碰撞損傷程度從能量角度看應該是相同的(撞完之後一樣熱)。另外說一點,這也是為什麼加速器常使用對撞的方式的緣故------為了提高相對動能亦即有效能量在總能量中所佔有的比例。
為何等我畢業了,才知道原來可以在這裡問作業。
彈碰,二者動能都不損失。恢復因子為1完全非彈碰,二者損失動能一樣。恢復因子為0取一個中間值,恢復因子0.5,恢復因子是碰後相對速度比碰前相對速度,即相對速度都是2v,碰後相對速度都是v,設速度v,質量m,變數e=mv2模型1,離開速度各自為1/2*v模型2,碰後速度分別為3/2*v,和1/2*v所以,模型1損失動能3/4*e,模型2損失動能3/4*e,兩個模型還是一樣的。這裡給個結論吧碰撞的動量損失E=1/2*摺合質量*(1-恢復因子2)*碰前相對速度2,摺合質量為質量1乘質量2除以二者之和。如果把破壞程度等價於動能轉變為內能的量,且碰撞模型的幾何尺寸影響可以忽略(最好可以是等價於小球碰小球,畢竟和小球碰膜肯定不同),那麼題設給出的條件下任何碰撞,只要相對速度相等,摺合質量相等,恢復因子相等,破壞程度也相等。
推薦閱讀:
※用手按壓一個玻璃圓珠一側,圓珠往前方滾去,為什麼跑一段距離後,會往回退,這屬於什麼物理學運動類型?
※為什麼水面結冰都是從邊緣向中間結?
※在中國科學技術大學讀書是一種怎樣的體驗?
※一輛 50 噸重的坦克,和一輛 100 噸重的卡車以 50 公里/時的速度正面對撞,會有什麼後果?
※代數拓撲在物理學中有哪些應用?
