怎麼理解貝塞爾曲線？

---

貝塞爾曲線掃盲 把這篇文章看完你就知道了：）

---

貝塞爾曲線(Bézier curve)，又稱貝茲曲線或貝濟埃曲線，是應用於二維圖形應用程序的數學曲線。

由於用計算機畫圖大部分時間是操作滑鼠來掌握線條的路徑，與手繪的感覺和效果有很大的差別。即使是一位精明的畫師能輕鬆繪出各種圖形，拿到滑鼠想隨心所欲的畫圖也不是一件容易的事。這一點是計算機萬萬不能代替手工的工作，所以到目前為止人們只能頗感無奈。使用貝塞爾工具畫圖很大程度上彌補了這一缺憾。

貝塞爾曲線貝塞爾曲線是計算機圖形圖像造型的基本工具，是圖形造型運用得最多的基本線條之一。它通過控制曲線上的四個點（起始點、終止點以及兩個相互分離的中間點）來創造、編輯圖形。其中起重要作用的是位於曲線中央的控制線。這條線是虛擬的，中間與貝塞爾曲線交叉，兩端是控制端點。移動兩端的端點時貝塞爾曲線改變曲線的曲率（彎曲的程度）；移動中間點（也就是移動虛擬的控制線）時，貝塞爾曲線在起始點和終止點鎖定的情況下做均勻移動。注意，貝塞爾曲線上的所有控制點、節點均可編輯。這種「智能化」的矢量線條為藝術家提供了一種理想的圖形編輯與創造的工具。

以下公式中：B(t)為t時間下 點的坐標；

P0為起點,Pn為終點,Pi為控制點

一階貝塞爾曲線(線段)：

意義：由 P0 至 P1 的連續點， 描述的一條線段

二階貝塞爾曲線(拋物線)：

原理：由 P0 至 P1 的連續點 Q0，描述一條線段。

由 P1 至 P2 的連續點 Q1，描述一條線段。

由 Q0 至 Q1 的連續點 B(t)，描述一條二次貝塞爾曲線。

經驗：P1-P0為曲線在P0處的切線。

三階貝塞爾曲線：

通用公式：

高階貝塞爾曲線：

4階曲線：

5階曲線：

---

bezier 其實很簡單~

### 一階貝塞爾（直線）

一階貝賽爾曲線上的由兩個點確定 P0 和P1,當t在0---&>1區間上遞增時，根據

此會得到多個點的坐標，其實這些的點就是一條直線上的點。

B(t) = P0 + (P1-P0)*t
B(t) = (1-t)P0 + tP1
//=&>
B(t).x = (1-t)P0.x + tP1.x
B(t).y = (1-t)P0.y + tP1.y


### 二階貝塞爾（曲線）

二階貝賽爾曲線由`3`個點確定，它可以理解成是這樣的一階貝賽爾曲線：確定該`一階貝賽爾曲線`的兩個點是變化的。

這兩個點（設分別為Pm,Pn）是怎樣變化的呢，這兩個點又分別是(P0,P1)確定的`一階貝賽爾曲線`和(P1,P2)確定的`一階貝賽爾`

曲線上的點。

於是有了2階貝賽爾曲線的公式

Pm(t) = (1-t)P0 + tP1
Pn(t) = (1-t)P1 + tP2
B(t) = (1-t)Pm(t) + tPn(t)
= (1-t)^2 P0 + 2(1-t)tP1+ t^2P2



### 三階貝塞爾曲線

三階貝塞爾曲線由`4`個點確定，它可以理解成這樣的二階貝塞爾曲線：確定該二階貝賽爾曲線的三個點事變化的，

這三個點（Px,Py,Pz）是怎樣變化的呢，這三個點分別是P0+P1/P1+P2/P2+P3的確定的一階貝塞爾曲線上的點。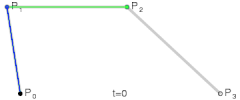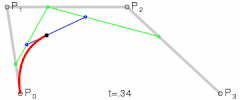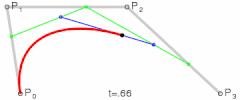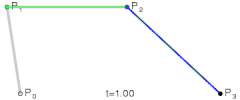


### 總結

2點確定一個點(隨著t變化)

3點確定2個點

4點確定3個點

5點確定4個點

無限延伸，就像二進位可以延伸出我們美麗計算機世界一樣。


### 實現

原理講完了，讓我們來用 JavaScript 實現一個 bezier 曲線~

function bezier(pots, amount){
var pot;
var lines;
var ret = [];
var points;
for(var i = 0; i &<= amount; i++){ points = pots.slice(0); lines = []; while(pot = points.shift()){ if(points.length){ lines.push( pointLine([pot, points[0]], i / amount) ); }else if(lines.length &> 1){
points = lines;
lines = [];
}else{
break;
}
}
ret.push(lines[0]);
}
function pointLine(points, rate){
var pointA, pointB, pointDistance, xDistance, yDistance, tan,radian, tmpPointDistance;
var ret = [];
pointA = points[0];
pointB = points[1];
xDistance = pointB.x - pointA.x;
yDistance = pointB.y - pointA.y;
pointDistance = Math.pow(Math.pow(xDistance, 2) + Math.pow(yDistance, 2), 1/2);
tan = yDistance / xDistance;
radian = Math.atan(tan);
tmpPointDistance = pointDistance * rate;
ret = {
x: pointA.x + tmpPointDistance * Math.cos(radian),
y: pointA.y + tmpPointDistance * Math.sin(radian)
};
return ret;
}
return ret;
}


---

主要是工業製圖用的，需要一種繪製曲線的方式，並且可以方程化。

---

您好，大神。擬合出來的三次參數方程後，怎麼判斷它是具體的一個怎樣的方程。比如x=t，y=t^3，我們直觀看出y是關於x的一元三次方程，如果複雜一點，x=a*t^3+b*t^2，y=c*t^3+d*t^2，我們又怎麼確定它大致的是一個怎樣的方程呢？

---

推薦閱讀：